Аннотация

Разработана Теория Комплексных Множеств. Проведено первичное исследование свойств Комплексных множеств, как новых математических объектов. Теория Комплексных Множеств может оказаться полезной при моделировании и исследовании свойств биологических, психологических и социальных систем, а также сложных иерархических технических и природных систем. Первоначально Теория Комплексных Множеств, появилась при исследовании связи семантических символов и их прообразов в реальном физическом мире. Настоящее исследование показало практическую полезность и эвристическую ценность Теории Комплексных Множеств (ТКМ). В статье излагается первый этап исследования Комплексных Множеств. Приведены некоторые полезные теоремы для ТКМ. Рассмотрены Комплексные Числа, как частный случай Комплексных Множеств. Введены несколько новых понятий для Комплексных Множеств – внутренние отображения, родственность. Введены в рассмотрение новые типы универсальных множеств, таких, как универсальные множества артефактов. Показана особая аналитическая роль между КМ, имеющими пересекаемость внутренних множеств.

Ключевые слова

Комплексные числа, Комплексные множества, пространство мнимых множеств, теория комплексных множеств, Теория множеств, множества, универсум комплексных множеств, комплексное пустое множество, булеан комплексного множества, комплексная мощность комплексного множества, скалярная мощность комплексного множества, отображение комплексного множества, числовые комплексные множества, вещественная часть комплексного множества, мнимая часть комплексного множества, множество всех артефактов, множество всех символов и образов, множестве всех созданных материальных предметов, внутренние множества комплексного множества, родственность комплексных множеств, внутренняя пересекаемость комплексных множеств

Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках.
Давид Гильберт

Сокращения, обозначения, нотация комплексных множеств

Сокращения

КМ – Комплексные Множества
ТКМ – Теория Комплексных Множеств
КЧ – Комплексные Числа

Нотация Комплексных Множеств

Здесь и далее вводим понятие Комплексное Множество и обозначаем его следующим образом:
(1) X=A+Bi
где: A, B – множества или семейства произвольных множеств; i – мнимая единица отвечающая формуле:
(2)  i² = -1
Множество A будем называть вещественной частью КМ; множество B будем называть мнимой частью КМ, i – будем называть мнимой единицей. Оба множества A и B будем называть внутренними множествами Комплексного Множества.
Далее все КМ и их внутренние множества A и B будем обозначать заглавными буквами.

Обозначения

В статье будут рассматриваться в качестве примеров три Комплексных Множества X, Y, Z со значениями:
X=A+Bi
Y=C+Di
Z=E+Fi
Возможно переназначение КМ X, Y, Z других значений – это всегда будет делаться явно.
Иногда, для напоминания, значения X, Y, Z будут повторно показываться в тексте статьи.

Определение Комплексного Множества

Комплексным Множеством Z называется множество или семейство множеств следующего вида:
Z = {a₁,…a_n }+{b₁,⋯b_m }i
где: a_i и bj  – это элементы произвольных множеств и i² = -1
или:
(4) Z = A + Bi где: A = {a_i}ⁿ_i=1 ∧ B = {b_j }^m_j=1 ∧  i² = -1

Мнимая единица i является полным аналогом мнимой единицы Комплексного Числа
Множества A и B назовём внутренними множествами Комплексного Множества.
Дополнительно семейства КМ можно обозначить как:
(5) Z={A}+{B}i

Отношения между КМ

Пусть даны КМ: X=A+Bi;  Y=C+Di
Объединение КМ X и Y:
X ∪ Y=(A+Bi) ∪ (C+Di) = (A ∪ C) + (B ∪ D)i
Пересечение КМ:
X∩Y=(A+Bi) ∩ (C+Di) = (A ∩ C) + (B ∩ D)i
Равенство КМ:
(X = Y) ⇔ ((A=C)∧(B=D))

Мощность КМ:

Мощность множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные. Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким. Мощность множества A обозначим |A|.

У КМ есть два типа мощности:
1. Скалярная мощность КМ
2. Комплексная мощность КМ
Пусть дано КМ X=A+Bi. Тогда скалярная мощность КМ X обозначается как |X| и есть сумма мощностей множеств А и B
|X|= |A|+|B|
Комплексная мощность КМ обозначается |X|_i или |X|(i) и является комплексным числом, у которого вещественная часть, это мощность множества A, а мнимая часть, это мощность множества B: |X|(i)=|A|+|B|i

Пустое КМ

Обычное пустое множество обозначается ∅. Пустое КМ обозначим как ∅(i) и теперь мы можем его представить в следующем виде:
∅(i) = ∅ + ∅i
Нам недостаточно обычного пустого множества ∅ для определения пустого КМ, так как вещественная часть КМ может быть равна ∅, а мнимая быть не пустым множеством и это должно быть представлено. Поэтому пустое КМ ∅ (i) состоит из обычного, вещественного пустого множества ∅ и мнимого пустого множества ∅i.
Операции с пустым КМ и КМ X:
X ∪ ∅(i)=X
X ∩ ∅(i)=∅(i)

Вынести в дополнения

Комплексные числа

Важно упомянуть, что обычное Комплексное Число является частным случаем Комплексного Множества. Этот частный случай реализуется тогда, когда мощность множеств А и В равна 1, а элементами обоих множеств являются только вещественные числа:
∀a∀b{Z|Z = A + Bi ∧ a ∈ A ∧ b ∈ B ∧ (|A| = |B| = 1) ∧ (a ∈ ∧ b ∈ )}
где – множество всех вещественных чисел
Комплексное Множество не следует путать с множеством комплексных чисел.
Комплексные Числа – это числа вида z=a+bi, где a и b вещественные числа:
∀a∀b {z|z = a + bi, a ∈ ∧ b ∈ ∧ i²= -1}
Для КМ можно применить аналогичную формулу:
∀A∀B {Z|Z = A+Bi (A ⊂ ⋃ ∧ B⊂⋃ ∧ i²=-1)}
где ⋃ – универсальное множество всех Множеств.

Универсальным называется множество, которое содержит все возможные элементы, встречающиеся в данной задаче. Универсальное множество обозначается символом U.

Обычные множества

Множество всех комплексных чисел обозначается обычно как .

Множество всех КМ и Универсум КМ

Аналогично можно ввести понятие множества всех КМ и обозначить его, например:
{C} или  C(i)
Тогда множество всех комплексных чисел является подмножеством множества всех КМ (ниже будет показано, что КЧ является частным случаем КМ):
C ⊂ C(i)
Универсум КМ как множество всех КМ можно было бы обозначать как:
{U}i или {}^U или {i} или U(i)
Но понятие Универсума после того, как определены КМ должно включать все типы множеств, включая КМ и КЧ и тогда обозначение универсума может сохранить своё обозначение как U и при этом мы понимаем, что U стал рассматриваться шире, чем раньше.

Отношения М и КМ

С ∈ (A+Bi) ⇒ С = A ∨ C = B
C ⊆ (A+Bi) ⇒ (C ⊆ A ∨ C ⊆ B) ∨ (C ⊆ A ∧ C ⊆ B)
Можно рассмотреть и такое правило:
C ⊆ (A+Bi) ⇒ C ⊆ (A ∪ B) A ⇒ [C ⋐ (A+Bi)]
В последней формуле альтернативная нотация этого случая приведена в квадратных скобах

Родственность КМ

Выяснилось, что при применении КМ играют важную роль отображения КМ. Отображения эффективны как для внутренних множеств КМ, так и между разными КМ.

Отображение множества А в множество В это соответствие, в силу которого каждому элементу х множества А соответствует определённый элемент у = f (x) множества В.  у называют образом элемента х (элемент х называют прообразом элемента у). Иногда под О. понимают установление такого соответствия.

Поэтому оказалось важным обратить внимание на различные соотношения внутренних множеств КМ или возможность биективного отображения КМ, а также эти же возможности для разных КМ.

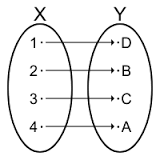
При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Биективное отображение называют также взаимно однозначным отображением (соответствием).

Поэтому были выделены для классификации следующие случаи:

Родственные КМ

Пусть даны КМ X и Y.
Родственными КМ мы назовём такие КМ, у которых хотя бы одна пара внутренних множеств из разных КМ равна друг другу:
A = C ∨ A = D ∨ B = C ∨ B = D

Биективно-родственные КМ

Биективно-родственные КМ, это такие КМ, у которых по крайней мере одна пара внутренних множеств из разных КМ имеет равную мощность, что позволяет провести между некоторыми внутренними множествами двух КМ биективное отображение
|A| = |C|∨|A| = |D|∨|B| = |C|∨ |B| = |D| уточнить

Тождественно-родственные КМ

(A=В)

Внутренне биективно-родственные КМ

|A|=|B|

Основные операции над КМ

Пересечение (множество общих точек)

Пересечение для обычных М:
A∩B = {x|x ∈ A ∧ x ∈ B}
Пересечение семейства М.
Пусть дано семейство множеств {M_α}_α∈A. Тогда его пересечением называется множество, состоящее из элементов, которые входят во все множества семейства:
⋂_α∈A M_α = {x| ∀α ∈ A, x ∈ M_α }

Пересечение КМ

Пересечение КМ в общем случае:
X∩Y = A∩C + (B∩D)i

Объединение КМ

Для обычных множеств
A ∪ B = {x,y|x ∈ A, y ∈ B}
Для КМ:
X ∪ Y = (A+Bi) ∪ (C+Di) = A ∪ C + (B∪D)i

Разность КМ

Для обычных множеств:
A∖B = {x ∈ A|x ∉ B}
— это множество называется дополнением B до A и обозначается:
A^C, Ā, A^‘,C_xA  
Ā = A ∖ B  
Для КМ X, Y:
X ∖ Y =  A ∖ C + B ∖ D
∀a∀b∀c∀d(a ∈ A ∧ b ∈ B ∧ c ∈ C ∧ d ∈ D)
{x ∈ a|x ∉ c} + {y ∈ b|y ∉ d}i

Симметрическая разность КМ

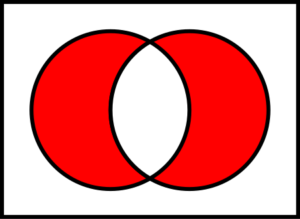
Симметрическая разность множеств – это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Также симметрическую разность можно рассматривать как разность между объединением и пересечением исходных множеств. Другими словами, если есть два множества A и B, их симметрическая разность есть объединение элементов A, не входящих в B, с элементами B, не входящими в A.
На письме для обозначения симметрической разности множеств A и B используется обозначение A Δ B, , реже используется обозначение A − B.

XΔY ≡ X – Y = (X ∪ B) ∖ (X ∩ Y)

Другие отношение КМ:

X⊂Y⇔(A⊂C)∧(B⊂D)
X⊆Y⇔((A⊆C)∧(B⊆D))
X∖Y=A∖C+(B∖D)ⅈ
(X=Y) ⇔(Y=X)
(X∩Y)=(Y∩X)
(X∪Y)=(Y∪X)
(X∪Y)∪Z= X∪(Y∪Z)
(X∩Y)∩Z= X∩(Y∩Z)
(X=Z)∧(Y=Z) ⇒(Y=X)

 

Теоремы для пересечений КМ в частных случаях

Интересен анализ пересечений двух КМ, когда их внутренние множества могут пересекаться соответственно их типу.

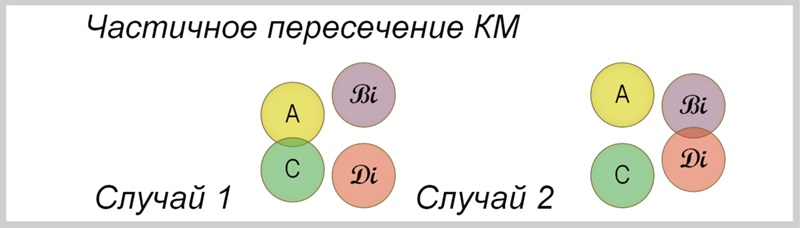
Для частично пересекающиеся КМ есть два случая:
Случай 1
(A ∩ C ≠∅) ∧ (B ∩ D = ∅)
∀X∀Y((A ⊂ C) ∧ (B ∩ D = ∅)) ⇒ (X ∩ Y = A) ∧
( X ∪ Y = C + (B ∪ D)i)
Случай 2:
(A ∩ C = ∅) ∧ (B ∩ D ≠ ∅)
∀X∀Y((A ∩ C = ∅) ∧ (B ∩ D ≠ ∅)) ⇒ (X ∩ Y = Bi) ∧
(X ∪ Y = A ∪ C + Di)

К началу страницы

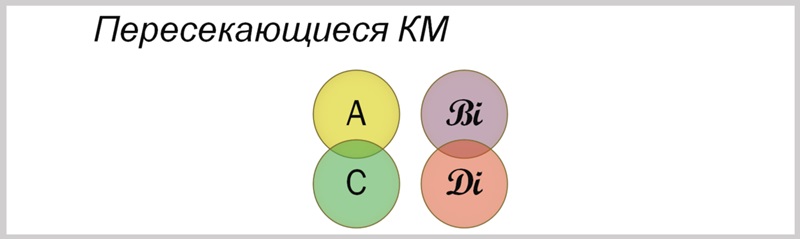
(53) (A ∩ C ≠ ∅) ∧ (B ∩ D ≠ ∅)
(54) ∀X∀Y((A ∩ C ≠ ∅) ∧ (B ∩ D ≠ ∅))⇒
X ∩ Y = (A ∩ C + (B ∩ D)i) ∧
X ∪ Y = (A ∪ C + (B ∪ D)i)

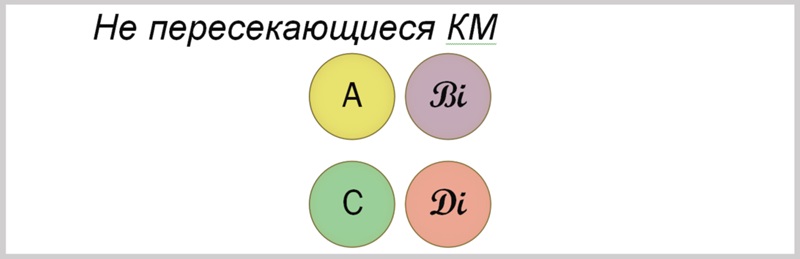
(A ∩ C = ∅) ∧ (B ∩ D = ∅)
∀X∀Y((A ∩ C = ∅)) ∧ (B ∩ D = ∅)) ⇒ X ∩ Y = ∅(i)
Операция пересечения КМ коммутативна:
X ∩ Y = Y ∩ X
Операция пересечения КМ ассоциативна:
(X ∩ Y) ∩ Z = X ∩ (Y ∩ Z)
Операция пересечения КМ дистрибутивная относительно операции объединения КМ
(⋃_kX_k ) ∩ Y = ⋃_k(X_k ∩ Y)
Универсальное множество КМ U является нейтральным элементом операции пересечения КМ:
X ∩ U = X
Операция пересечения множеств идемпотентна:
Y ∩ Y = Y

Идемпотентная (“равносильность” от лат. idem “тот же самый” + potens “способный”) операция– это операция, которая при многократном вызове возвращает один и тот же результат.

Если ∅ пустое множество или ∅(i) пустое КМ, то:
Y ∩ ∅ = ∅
Y ∩ ∅(i) = ∅(i)

Числовые КМ

Пусть дано КМ X=A+Bi
Числовое КМ, это такое КМ, в котором оба внутренних множества КМ, и вещественное и мнимое, являются числовыми множествами:
∀a∀b {X|(X=A+Bi) ∧ a ∈ A ∧ b ∈ B ∧ a,b ∈ R}
Здесь можно говорить о точках с числовыми координатами A и B в соответствующих многомерных пространствах, которые связаны через комплексную плоскость. Естественно, что в большинстве случаев размерность пространств A и B может не совпадать. Если размерность пространств будет совпадать, то такие КМ мы будем называть родственными. Ниже такие КМ будут проанализированы.

Типы числовых КМ

Числовое КМ Z=A+Bi является:
– счётным если для него действительны следующие утверждения:
A ⊂ N и B ⊂ N
или
A → N и B → N
– рациональным если:
A ⊂ Q и B ⊂ Q
– вещественным, если:
A ⊂ R и B ⊂ R
(не путать: вещественная часть КМ и вещественное число)
– Числовым смешанным, если A и B будут множествами с разными типами чисел, например:
A → N ∧ B → Q
A ⊂ R ∧ B ⊂ Q и т.д.
Числовые КМ могут быть бесконечными:
Если A = [0, R) ∧ B = [0,R), то X = A+Bi описывает декартову систему координат без отрицательных значений или плоскость, начинающуюся от нуля и ограниченную двумя перпендикулярными прямыми.
Если A = (-R, R ) ∧ B=(-R, R), то X=A+Bi описывает декартову систему координат или бесконечную двумерную декартову плоскость.

Комплексные числа как частный случай КМ

Комплексное число z=a+bi. Множество комплексных чисел обозначается C. z=a+bi можно рассматривать как КМ, в котором a и b являются внутренними множествами A и B КМ из одного элемента причём a и b являются исключительно только числами. Например:
X = A+Bi, где A=a, B=b и a ∈ R, b ∈ R, i² = -1

Обычные множества

Обычные множества является частным случаем КМ.
Пусть дано произвольное КМ X=A+Bi. Если B=∅, то X – обычное множество, равное A.
Если мы выделим два универсума для множеств: обычный универсум U и комплексный универсум U(i), то
(X = A+Bi) ∀ A ∈ U ∧ ∀ B = ∅) ⇒ X ∈ U
Иначе:
(X = A+Bi) ∀ A ∈ U ∧ ∀B = U ∧ ∀B ≠∅) ⇒ X ∈ U(i)

Отображения в КМ: Связь вещественной и мнимой части КМ

Общий случай

Приведённый нами пример использования КМ в семантических связах слова «стул» и реальных стульев, подразумевает сильную связь, через механизм отображений между вещественным стулом и мнимым стулом.
В семантическом случае отображение не обязательно является биективным потому, что:
1. Могут быть объекты ещё не названные, или не открытые в вещественной реальности, то есть объекты есть, но в мнимом пространстве их нет.
2. Могут быть символы ещё не созданных предметов, символы-проекты, то есть объекты согласно их смыслу ещё не существуют или не будут созданы никогда, например, симулякры.

Симулякр (фр. simulacre от лат. simulacrum — подобие, копия) — термин, который означает изображение, копию того, чего на самом деле не существует. Симулякр может касаться каких угодно вещей и смыслов.

Пусть Z=M+Ni произвольное КМ, в котором M и N произвольные множества какой угодно природы. «Тогда на множестве M определена функция f, принимающая значения из множества N. Вместо термина «функция» часто пользуются термином «отображение». При специализации природы множеств M и N возникают специальные типы функций, которые могут носить особые названия «вектор-функция», «мера», «функционал», «оператор» и т. д…» [Элементы теории функций и функционального анализа, А. Н. Колмогоров, С. В. Фомин. Главная редакция физико-математической литературы изд-ва «Наука», М., 1976 г].
В случае КМ в реальных случаях возникают отображения как из M в N так и наоборот из N в M.

Общий случай

Дано два КМ X и Y, тогда может быть создано отображение X в Y
f: X → Y ⇒ (f: A → C) ∧ (f: B → D)

Внутреннее отображение КМ. Эффективность внутренних отображений

Дано X=A+Bi
f : A → B ⇒ {b = f(a) | b ∈ B ∧ a ∈ A}
В реальных семантических КМ, которое мы предложили в качестве примера, могут быть все типы отображений: сюръективное, биективное, инъективное – как уже указывалось, могут быть вещественные элементы, которые не имеют связей с мнимыми элементами и наоборот. В первом случае, мы говорим, что объект в вещественном мире есть, а образа в сознании человека нет; во втором случае мы говорим, что образ или проект вещи есть, но самой вещи ещё нет. Во всех остальных случаях существуют какие-то связи внутри КМ между вещественным множеством и мнимым.

Философия внутренних отображений КМ

Для комплексных чисел предполагается, что каких-то дополнительных связей между вещественной и мнимой частями не существует.
Для КМ сам процесс формирования их концепции начался с того, что может существовать связь через отображение между вещественной и мнимой частями внутри одного КМ. Во многих случаях эта связь поддерживается через сознание человека.
Наше исследование показало, что инструмент внутренних отображений КМ хорошо работает в моделировании биологических, психологических, лингвистических и социальных иерархических системах.
Пусть дано КМ X=A+Bi. Тогда внутренними отображениями КМ множества X являются отображения A→B или B→A:
f: A → B ⇒ {b = f(a) | b ∈ B ∧ a ∈ A}
f: B → A ⇒ {a = f(b) | a ∈ A ∧ b ∈ B}

Типы внутренних отображений:

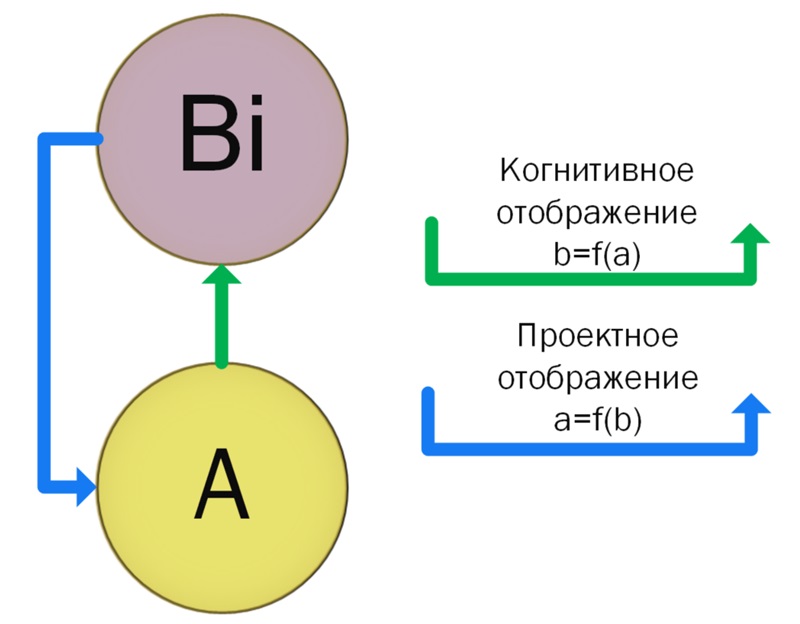
Рассмотрим взаимодействие множества свойств вещественного стула (A – ОЯ) с множеств (мнимых, не вещественных) свойств образа стула (B – ОЯ) в сознании человека. Могут быть различные сценарии возникновения КМ «Стул»:
Сценарий 1. Однажды интуитивно возникший предмет стул получает своё название – слово «стул». В этом случае мы имеем процесс аналитического создания семантического множества, образа вещественного стула в мнимом пространстве человеческого сознания. Физический стул отражается, отображается в сознании человека. Назовём этот тип отображения «Когнитивное отображение».
Сценарий 2. По мере развития цивилизации предмет может быть придуман, изобретён человеком, а после этого будет создан в вещественном мире. Назовём этот тип отображения «Проектное отображение». (Сначала проект – потом изделие)
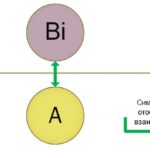
Необходимо отметить, что внутри КМ, описывающего реальные явления, пролегает граница обособленности, смены среды или уровня иерархии, в том числе и в эволюционных иерархических системах:

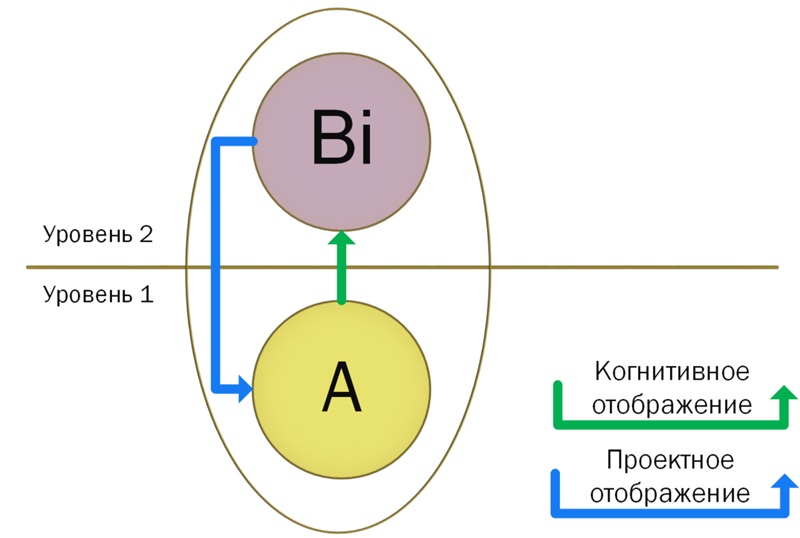
В данном описанном случае Уровень 1 соответствует физическому, вещественном миру, а Уровень 2 – сознанию человека.
Таким образом мнимая единица i, позволяет аналитически обособить друг от друга множества свойств и параметров, принадлежащих к разным иерархическим уровням одной системы или к разным связанным системам.
Мы видим, что КМ внутри себя может иметь границу – границу внутри двойственности. Мнимость I получает интересное философское трактование:

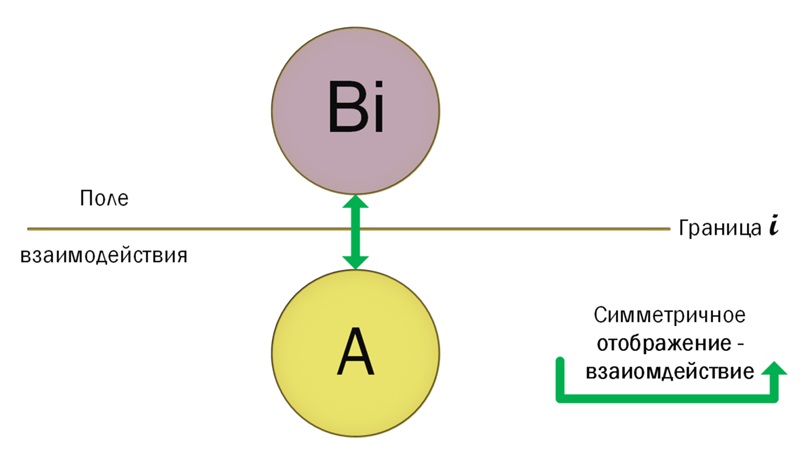
Пусть даны два КМ X=A+Bi и Y=C+Di , а также дана четырёх уровневая система, где уровни соответствуют различным уровням иерархии или эволюции. КМ наложенные на эту систему иллюстрируют возможность их применения для описания связей между множествами свойств объектов на каждом уровне:

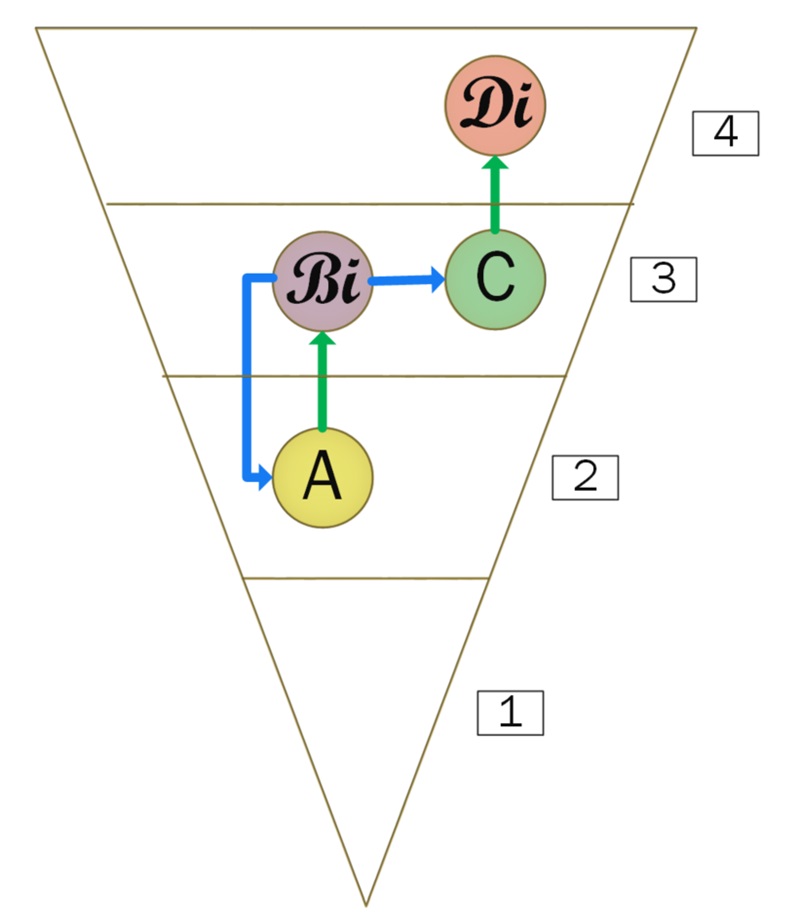
На рисунке мы видим, как КМ покрывающие разные уровни четырёхуровневой системы могут пронизывать всю систему и описывать иерархию свойств и связи уровней. Следует обратить внимание, КМ X начинается своей вещественной частью A на Уровне 2 идёт своей мнимой частью на Уровень 3, который для Уровня 2 является мнимым (в нём располагается мнимая часть X), и тут же начинается КМ Y, в котором располагается его вещественная часть С, а его мнимая часть D располагается уже на Уровне 4, для которого Уровень 3 является вещественным.
В заключение этого раздела следует отметит, что природа КМ позволяет показать в виде двойственности физический предмет и его отражение (как отображение), например, в сознании в виде замещающего символа предмета. Видим, что внутренние отображения КМ позволяют моделировать явления связи между множествами находящимися на разных уровнях иерархии или в разных системах.

Булеан

Булеан — это множество всех подмножеств A, включая пустое множество и само множество A. Булеан множества обозначается как P(A), где A — исходное множество. Мощность булеана множества равна 2ⁿ, где n — мощность исходного множества. Например, если множество A содержит 3 элемента, то булеан множества P(A) будет содержать 2³ = 8 элементов.

Дано КМ X=A+Bi.
Тогда Комп.Булеан КМ обозначаемый 2x(i)X будет равен:
P{X} = 2^x(i) = 2^A + 2^Bi
Булеан для КМ сам является КМ.
P{X} = P{A} + P{B}i
Ковариантный функтор отображает функцию f: A → B в функцию Pf: Pa → Pb такую, что она отображает X в образ X относительно f

Функтор — это общий термин, который используется для обозначения объекта или структуры данных, которая может быть вызвана или применена как функция. Функтор обычно используется для реализации различных операций над данными, таких как преобразования, фильтрации или комбинирования. Функтор (в математике) — особый тип отображений между категориями, который можно понимать как отображение, сохраняющее структуру.

Универсальное множество

Рассматривается универсальное множество U включающее в себя все множества. Мы исходим из практического использования КМ, которое опирается на факты, что количество предметов, например количество стульев на Земле ограничено, а также из того факта, что ёмкость памяти, как одного человека, так и всего человечества ограничена – не бесконечна. Поэтому для нашего примера все множества конечны. Тем не менее можно ввести бесконечное множество всех КМ для сохранения преемственности с ТМ. Также можно предположить, что Вселенных бесконечно много и тогда универсальное множество существует в более сложной реальности.

Re and Im

Вещественную часть КМ, аналогично КЧ можно обозначать Re(Z) а мнимую Im(Z)

Чисто мнимое КМ

Если A=∅ то Z чисто мнимое КМ.

Комплексная плоскость

Можно рассматривать КМ, как семейства из двух пар множеств относительно комплексной плоскости.

Альтернативная нотация

Пусть Z=A+Bi, тогда можно предложить другую нотацию:
Z = {A, Bi}
Также допустимо обозначение: (Не завершено автором – ОЯ)

Заключение

Мы надеемся, что предложенная в статье Теория Комплексных Множеств привлечет внимание математиков, физиков и других учёных для дальнейшего исследования возможностей Комплексных Множеств. В физике нам кажется интересным исследование взаимодействий через моделирование с помощью отображений в КМ. Нам представляется, что модель КМ может оказаться удобной в некоторых случаях моделирования сложных систем. Также мы предполагаем, что Теория КМ имеет когнитивное и философское значение. В философии интересно рассмотреть тринитарный подход (два объекта и взаимодействие – как неделимый комплекс) к анализу любых взаимодействий.
В дальнейшем мы планируем рассмотреть в следующей статье такие темы:
1. Битовые КМ (кватернионы).

Кватернион — это ось, относительно которой вращается объект и угол, на который мы будем вращать объект относительно этой оси. Всего у кватерниона четыре компоненты: X, Y, Z и W. Кватернионы предложены Уильямом Гамильтоном в 1843 году. Кватернионы удобны для описания изометрий трёх- и четырёхмерного евклидовых пространств и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике — например, при создании трёхмерной графики.

2. Применение КМ в семантических сетях.

К началу страницы

Таблица используемых математических символов

∀ квантор всеобщности (\forall, «Для любых», «Для всех», «Для всякого»);
| множество элементов, удовлетворяющих условию («Множество всех… таких, что верно…»);
∧ «и» (\wedge, Конъюнкция);
∨  Дизъюнкция (\vee, «или», A ∨ B истинно, когда хотя бы одно из условий A или B истинно.)
∈ принадлежность к множеству (\in, «принадлежит», «из»);
⋃ Объединение (\cup, «Объединение … и …», «…, объединённое с …», A ⋃ B означает множество, содержащее все элементы из A и B);
∩ Пересечение (\cap, «Пересечение … и …», «…, пересечённое с …», A ∩ B означает множество одинаковых элементов, принадлежащих и A, и B);
⊂  Подмножество (\subset, «является подмножеством», «включено в») (A ⊂ B обычно означает то же, что и A ⊆ B);
⊆ Подмножество (\subseteq, A ⊆ B означает «каждый элемент из A также является элементом из B».)
Импликация, следование (\Rightarrow, A B означает «если A верно, то B также верно».);
⋐  Двойное подмножество (Double Subset), представленное как ⋐, — это математическое обозначение, часто используемое в теории множеств. Этот символ представляет концепцию, в которой один набор не только является подмножеством другого, но также, возможно, равен ему;
∖  Разность множеств (\setminus, «разность … и …», «минус», «… без …», A ∖ B означает множество элементов, принадлежащих A, но не принадлежащих B, {1,2,3,4) \ {3,4,5,6} = {1,2});
⇔ Равносильность (\Leftrightarrow, «если и только если» или «равносильно», A ⇔ B означает «A верно тогда и только тогда, когда B верно»);
<

N – Натуральные числа;
Z – Целые числа
Q– Рациональные числа;
R –   Вещественные (действительные) числа;
C – Комплексные числа;

 

Источники

– Таблица математических символов

К началу страницы

Теория Комплексных Множеств. Часть 2. Дополнения. Евгений Олевский.