Оглавление

IBM объявила о планах создания квантового компьютера, объемом 100 000 кубит к 2033 году, чтобы продвинуть квантовые вычисления в область полномасштабной работы.

Введение

Квантовый компьютер – это вычислительное устройство, в основе работы которого лежат такие труднопонимаемые явления квантовой механики, как квантовые суперпозиция (superposition) и квантовая запутанность (entaglement). В отличии от обычного компьютера, который является цифровой вычислительной машиной, квантовый компьютер, по своей природе – аналоговое устройство, в котором нет бинарных операций.

Аналоговая вычислительная машина (АВМ), представляет числовые данные при помощи аналоговых физических параметров (скорость, длина, напряжение, сила тока, давление), в отличие от цифровых вычислительных машин, для работы которых аналоговые данные преобразуются в цифровые, с помощью специального преобразователя “Аналог – код”. У аналоговых машин нет оперативной памяти для хранения компьютерной программы, позволяющей решать различные задачи. Аналоговая машина – это машина одного алгоритма, который жёстко определяется внутренним устройством АВМ и выполненными настройками (соединениями, установленными модулями, клапанами и т. п.). Даже для универсальных АВМ, решение новой задачи требовало перестройки внутренней структуры устройства.

Квантовый компьютер, как и привычный аналоговый компьютер, не может работать без обычного компьютера, который загружает в него исходные данные, управляет процессом вычисления и выгружает полученные в результате вычислений данные, представляя их пользователю.
Квантовый компьютер оперирует не битами (способными принимать значение либо 0, либо 1), а кубитами, имеющими значения одновременно и 0, и 1 (этот эффект возникает из-за принципа суперпозиции, изучаемый в квантовой механике). Это позволяет обрабатывать все возможные состояния одновременно, достигая существенного преимущества (квантового превосходства) над обычными компьютерами в ряде алгоритмов. Интересно посмотреть, как это чудо работает.

Построение квантового компьютера требует развития квантовой теории в области многих квантовых частиц, а так же проведения сложных экспериментов. Главным препятствием для стабильной работы квантовых компьютеров является высокий уровень шумов, не позволяющий поддерживать нужное состояние квантовых объектов (даже трудно представить их микроскопический размер), достаточно долго для работы практических алгоритмов. И одна из важнейших задач – охлаждение “сердца” квантового компьютера до температуры, близкой к абсолютному нулю (– 273⁰ С).

Охлаждение квантового компьютера. Ранее, для поддержания температуры, близкой к абсолютному нулю, в квантовых компьютерах применялся чрезвычайно редкий и дорогой изотоп гелия-3 (³He). Сейчас применяются сжиженные инертные газы, что менее затратно, но все же дорого и сложно технически.

Если сравнить развитие квантовых компьютеров с традиционными компьютерами, то современные квантовые компьютеры находятся на уровне первых реализаций ламповых компьютеров в середине XX века, или ранее, в виде разработанного в середине 30-х – начале 40-х годов, немецким инженером Конрадом Цузе, электромеханического компьютера с программным управлением Z3. Как будут выглядеть квантовые компьютеры будущего – пока никто не знает.
Физическими системами, реализующими кубиты, могут быть любые квантовые объекты, имеющие два квантовых состояния:
– поляризационные состояния фотонов;
– электронные состояния изолированных атомов или ионов;
– спиновые состояния ядер атомов.

Электрон со спином ½ может пребывать в двух состояниях: спин вверх и спин вниз. Любая частица с таким свойством, будь то фотон, нейтральный атом или ион, может выступать в качестве кубита.

В настоящий момент уже существует ряд реализаций квантовых вычислений (кубитов), в скобках указаны компании – изготовители:
– сверхпроводящий контур (IBM, Google, Quantum Circuits);
– захваченные ионы (ionQ);
– кремниевые квантовые точки (Intel);
– топологические кубиты (Microsoft, Bell Labs);
– электронные дырки в кристаллах алмаза (Quantum Diamond Technologies).
На начало XXI века были построены единичные экспериментальные системы, исполняющие фиксированные алгоритмы относительно небольшой сложности.
В 2019 году, корпорация IBM представила первый в мире коммерческий, квантовый, 20-ти кубитный компьютер IBM Q System One.

20-кубитный компьютер IBM Q System One. Не похож на привычный компьютер.

IBM предлагает облачный доступ к самым современным квантовым компьютерам. Вы можете изучать, разрабатывать и запускать программы с помощью IBM Quantum Experience.
В 2020 году был заявлен китайский квантовый, 24-х кубитный компьютер «Цзючжан», работающий на запутанных фотонах, который достиг квантового превосходства при решении конкретной задачи. А именно: за 200 секунд было успешно проведено вычисление задачи, для решения которой, самому быстрому в мире классическому суперкомпьютеру, потребовалось считать бы более нескольких сотен миллионов лет.

Запутанные фотоны (элементарные частицы, переносящие электромагнитное взаимодействие и, в частности, свет) – это пара частиц, которые находятся в скоррелированных (запутанных) квантовых состояниях. Два, определённым образом полученных фотона, оказываются связаны между собой таким образом, что изменение состояния одного из них вызывает мгновенное изменение в состоянии другого, даже если они находятся на большом расстоянии друг от друга. Запутать фотоны и сохранить их запутанность при неизбежном взаимодействии с окружающим миром – задача сложная. Перепутанные состояния типичны и повсеместны. Но для большинства частиц, взаимодействие с окружением быстро разрушает перепутывание. Фотоны же практически ни с чем не взаимодействуют, поэтому они являются очень удобным объектом для использования.
Для получения пары запутанных фотонов, кристаллы с определёнными оптическими свойствами облучают, так называемым, лазером накачки. Фотон из лазерного пучка, попадая в кристалл, распадается на два фотона, энергия которых в сумме равна энергии фотона накачки. В силу законов сохранения, фотоны оказываются коррелированы, или запутаны.

К началу страницы

Что скажет IBM?

IBM объявила о планах создания квантового компьютера, объемом 100 000 кубит, к 2033 году. Компания будет сотрудничать с Токийским и Чикагским университетами, в рамках инициативы стоимостью 100 миллионов долларов, чтобы продвинуть квантовые вычисления в область полномасштабной работы. Только в таком случае, технология сможет решать насущные проблемы человечества, которые не под силу ни одному стандартному суперкомпьютеру.

А что в России

Российские физики, в 2023 году, создали российский квантовый компьютер на базе 16 сверхпроводящих кубитов, самый мощный квантовый компьютер в стране. Сейчас 16 кубитов есть на нескольких платформах, при этом, наибольшую вычислительную мощность показывает ионный процессор. До конца 2024 года, планируется увеличить число кубитов в отечественных вычислительных машинах до 50-100. Правительство РФ выделило 24 млрд рублей на исследования квантовых технологий. Поближе с положением квантовых дел в России можно познакомиться на странице: Квантовые компьютеры и сети в России.

В чём принципиальное отличие квантового компьютера.

Попробуем разобраться в том, что такое квантовый компьютер, в чём его принципиальные отличия от, так привычных нам и любимых компьютеров, прошедших за свою жизнь более пяти поколений. И начнём с того, что произошло с двоичным битом, цифровым сердцем компьютера, и как он умудрился превратиться в кубит.

Кубит

Кубит (Quantum Bit) – это наименьшая единица информации в квантовом компьютере (аналог бита в обычном компьютере), использующаяся для квантовых вычислений. Кубиты физически представлены квантовыми частицами. Жизнедеятельность кубита основана на законах квантовой механики, именно поэтому он может находиться в суперпозиции своих состояний. В 1995 году, Бенджамин Шумахер из Кеньон-колледжа, ввел термин q-bit (кубит).
Кубиты связаны между собой и имеют два состояния: суперпозиция и запутанность.
Суперпозиция кубита – это состояние, в котором возможна любая линейная комбинация элементов. Кубит, находящийся в суперпозиции, при измерении коллапсирует в одно из двух детерминированных состояний (0 или 1). Вероятность состояния 1 или 0 определяется суперпозицией кубита. Если кубит находится в равной суперпозиции, то он находится наполовину в состоянии 0, наполовину в состоянии 1.
??? Знающие люди образно говорят, что “кубит – это магнит (обычно атом или электрон), подвешенный в пространстве, который может вращаться по всем трем осям. Собственно, вращение магнита в пространстве – это и есть операции квантового компьютера.

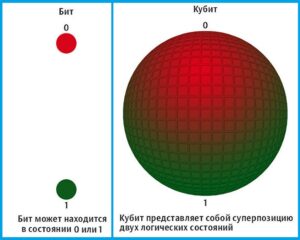Это одновременно открытая и закрытая дверь, или горящая и не горящая лампочка. Кубит, находится в суперпозиции, пока ты его не измеришь. Монетка – это пример суперпозиции: пока монетка в воздухе, она одновременно и орел, и решка, но как только её поймали, то все: либо орел, либо решка! То есть состояние определилось.”
Запутанные кубиты образуют систему, в которой все ее составляющие взаимно влияют друг на друга. Измерив один кубит, можно сделать выводы о всех оставшихся. Это в разы повышает скорость вычисления.

Одиночный кубит

Состояние одиночного кубита можно описать с помощью двумерного вектора-столбца единичной нормы, то есть сумма квадратов его элементов должна равняться 1. Этот вектор, называемый вектором квантового состояния, содержит всю информацию, необходимую для описания однокубитной квантовой системы, точно так же, как один бит содержит всю информацию, необходимую для описания состояния двоичной переменной.
Любой двумерный вектор-столбец с реальными или комплексными числами и нормой 1 представляет возможное квантовое состояние кубита.
Векторы – столбцы квантовых состояний [1 0] и [0 1] имеют особое значение, так как эти два вектора образуют вычислительную базу для векторного пространства, описывающего состояние кубита. А это означает, что любой вектор квантового состояния может быть записан как сумма этих базовых векторов. В частности, вектор [x y] может быть записан как x [1 0] + y [0 1]. Хотя любой поворот этих векторов будет служить вполне допустимой базой для кубита, выбран именно этот и назван вычислительной базой.
Эти два квантовых состояния выбраны для соответствия двум состояниям классического бита, а именно 0 и 1. Обычно выбирают:

0 ≡ [1 0] , 1 ≡ [0 1].

Хотя противоположный выбор также допустим, из-за неограниченного количества возможных векторов однокубитных квантовых состояний, только два из них соответствуют состояниям классических битов, чего нельзя сказать об остальных квантовых состояниях.

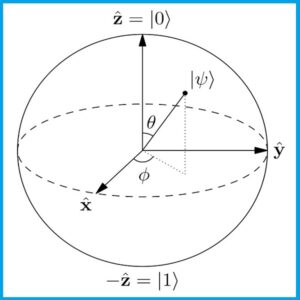
Состояние кубита удобно представлять как стрелку на сфере Блоха. Сфера Блоха является единичной двумерной сферой, каждая пара диаметрально противоположных точек которой соответствует взаимно ортогональным векторам состояния. Обычно предполагается, что северный и южный полюсы сферы Блоха соответствуют базисным Кет – векторам ∣ 0 ⟩ и ∣ 1 ⟩, которые в свою очередь могут отвечать, например, двум спиновым состояниям электрона («спин вверх» и «спин вниз»). Подобный выбор точек является произвольным. Точки на поверхности сферы соответствуют чистым состояниям квантовой системы, а точки внутри сферы представляют смешанные состояния.

Измерение кубита

Измерение является реализацией идеи “изучения” кубита, позволяющей моментально свернуть квантовое состояние в одно или второе классических состояния [1 0] или [0 1].
При измерении кубита, заданного с помощью вектора квантового состояния [α β], получаем значение 0 с вероятностью |α|² и значение 1 с вероятностью |β|². При значении
0 новым состоянием кубита является [1 0]; при значении 1 его состоянием является [0 1]. Важно, что сумма этих вероятностей равна 1 из-за условия нормализации |α|² + |β|² = 1.
Свойства измерения также означают, что общий знак вектора квантового состояния не имеет значения. Инвертирование вектора эквивалентно. Так как вероятность измерения 0 и 1 зависит от квадрата терминов, вставка таких знаков совершенно не влияет на вероятности.

Инвертирование вектора означает перечисление элементов вектора в обратном порядке.

Последнее важное свойство измерения заключается в том, что оно не обязательно приводит к повреждению всех векторов квантовых состояний. Если в начале у нас есть кубит в состоянии [1 0], что соответствует классическому состоянию 0, в результате измерения этого состояния мы всегда будем получать 0 и квантовое состояние останется без изменений. В этом смысле, если присутствуют только классические биты (например, кубиты со значениями [1 0] или [0 1] ), то измерение не приводит к повреждению системы.
Это означает, что можно реплицировать классические данные и управлять ими на квантовом компьютере точно так же, как на классическом компьютере.

Репликация – это процесс, под которым понимается копирование данных из одного источника на другой (или на множество других) и наоборот. При репликации изменения, сделанные в одной копии объекта, могут быть распространены в другие копии.

Кубит может находиться в суперпозиции, то есть хранить информацию в обоих состояниях одновременно. Поэтому, квантовый компьютер способен обрабатывать многовариантные состояния, а обычный компьютер просчитывает каждый вариант отдельно. Что и создает преимущество квантовых вычислений перед возможностями классических вычислений.

К началу страницы

Квантовые регистры

В квантовом компьютере регистр – это система из нескольких кубитов, точно так же, как в обычном компьютере в регистрах записывается набор битов. Квантовый регистр имеет размер, соответствующий числу кубитов в квантовом компьютере. Если двоичный регистр может содержать N битов (переключателей «включено-выключено»), то квантовый регистр тоже содержит N кубитов, над которыми можно производить различные квантовые операции. В упрощенной форме это можно представить так:

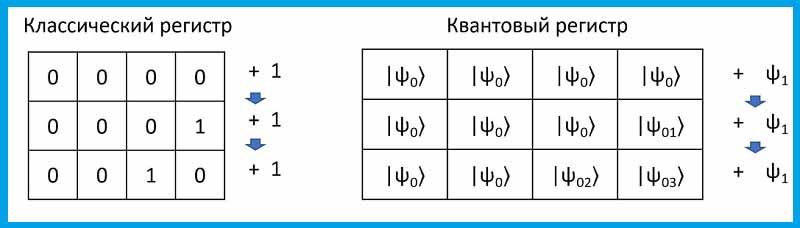
Классический (двоичный) регистр и квантовый регистр. В квантовом регистре расположены **Кет – вектора** состояний.

В квантовой теории “вектор состояния” или просто вектор обозначается символом ⟨ ∣ (Бра). Если какой-то набор данных, определяющих систему, обозначить буквой a, то вектор
состояния будет иметь вид ∣ a ⟩. В квантовой теории определяются два вида векторов состояний, называемые и обозначаемые “Бра” ⟨ ∣ и “Кет” ∣ ⟩ векторами.

Символы “Бра” ⟨ ∣ и “Кет” ∣ ⟩ и Векторы “Бра” ⟨ ∣ и “Кет” ∣ ⟩.

Бра ⟨ ∣ и кет ∣ ⟩ (англ. bra-ket: bracket ⟨ ⟩ скобка) – это алгебраический формализм, предназначенный для описания квантовых состояний. Называется также обозначениями Дирака. В матричной квантовой механике данная система обозначений является общепринятой и представляет собой иные текстуальные обозначения для векторов, ковекторов, билинейных форм и скалярных произведений. Потому формализм применим в линейной алгебре вообще. В тех случаях, когда речь идет о бесконечно-мерных пространствах и/или о линейной алгебре над комплексными числами. Символ “Бра”: ⟨ ∣ и символ “Кет”: ∣ ⟩.

Векторы “Бра” ⟨ ∣ и “Кет” ∣ ⟩.

Пусть имеется число α, которое будем считать соответствующим вектору ∣ a ⟩. Число α рассматривается в квантовой теории как “скалярное” произведение вектора ∣ a ⟩ на некоторый “новый” вид вектора. Эти “новые” векторы обозначаются символом ⟨ ∣. Если нужно обозначить этот вектор каким-то набором переменных, например b, то используется обозначение ⟨ b ∣. Скалярное произведение “нового” вектора ⟨ b ∣ и определенного ранее вектора состояния ∣ a ⟩ обозначается ⟨ b ∣ a ⟩. Такому скалярному произведению приписывается свойство комплексного числа. В квантовой теории принята следующая терминология: векторы
вида ∣ a ⟩ называются кет-векторами, а вида ⟨ b ∣ бра-векторами.
Введенное скалярное произведение должно обеспечить выполнение принципа суперпозиции, то есть быть линейной функцией состояния. Бра-вектор определен полностью, если задано его скалярное произведение с любым Кет–вектором. Так, например, если скалярное произведение равно нулю, то и сам Бра-вектор равен нулю.

Отличие квантового регистра от классического

Отличие квантового регистра в том, что он может хранить данные в состоянии суперпозиции, т.е. в вероятностном представлении. Пространство состояний N-мерного квантового регистра – это Гильбертово пространство из 2^N квантовых состояний.

Гильбертово пространство – это векторное пространство, состоящее из бесконечного числа взаимно ортогональных состояний, называемых базовыми состояниями или базисными векторами. Это обобщение Евклидова пространства, допускающее бесконечную размерность и полное по метрике, порождённой скалярным произведением. Названо в честь Давида Гильберта. Важнейшим объектом исследования в гильбертовом пространстве являются линейные операторы.

По мере увеличения числа кубитов происходит расширение Гильбертова пространства. То есть, если в классическом регистре записываются биты в виде 0 и 1, над которыми можно производить математические операции в двоичной форме, то в квантовом регистре записываются кубиты, которые являются своеобразными “векторными разрядами”, над которыми также можно производить операции, но уже векторные (матричные).
Классический регистр в один момент времени может находиться только в одном состоянии. Из-за этого для пересмотра всех вариантов ему приходится тратить время. Квантовый регистр в конкретный момент времени находится сразу во всех состояниях, а значит, можно получить результат практически моментально.

(Ниже пример трёх битового классического регистра и трёх кубитого квантового регистра. В конкретный момент времени N классический регистр хранит двоичное число 010, а квантовый регистр восемь двоичных значений от 000 до 111 – ОЯ)

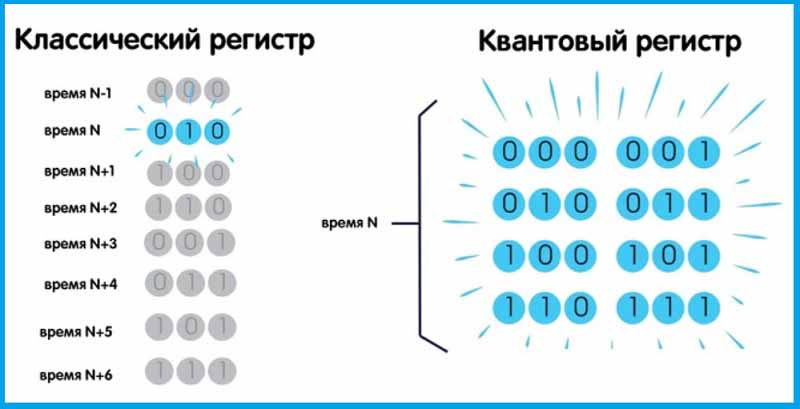
Квантовый компьютер задействует принцип вероятности. Устройство мгновенно анализирует все предполагаемые сочетания. Истинным становится наиболее реалистичное решение. Чаще всего оно и оказывается лучшим выбором.

К началу страницы

Квантовые вентили (Quantum gates)

В традиционных компьютерах используются электронные устройства в виде простейших логических элементов, способных выполнять элементарные логические задачи, которые являются основой интегральных цифровых микросхем. Входя в состав современных цифровых устройств (компьютеров, планшетов, смартфонов и пр.), они, в самых различных комбинациях, способны к реализации весьма сложных функций.
В квантовых вычислениях используются квантовые элементы — вентили (gates), которые выполняют основные квантовые операции. Квантовые вентили выполняют различные операции над кубитами, такие как логические, унитарные и нелинейные. Квантовые вентили используются для создания квантовых цепей и выполнения последовательности операций, составляющих квантовый алгоритм. Благодаря квантовым вентилям, получается достичь эффективности и гибкости квантовых вычислений.

Квантовый вентиль (квантовый логический элемент) – это базовый элемент квантового компьютера, преобразующий входные состояния кубитов в выходные по определённому закону. Отличается от обычных логических вентилей тем, что работает с кубитами. Квантовые вентили в отличие от классических всегда являются обратимыми. Набор квантовых вентилей называют универсальным, если любое унитарное преобразование можно аппроксимировать с любой заданной точностью конечной последовательностью вентилей из этого набора. Иными словами, универсальные квантовые вентили являются генераторами группы унитарных матриц. Можно доказать, что набор, состоящий из вентиля C-NOT и всех однокубитных вентилей, является универсальным. Возможны и другие универсальные наборы.

Так как кубит можно представить вектором в двумерном пространстве, то действие вентиля можно описать унитарной матрицей, на которую умножается соответствующий вектор состояния входного кубита.

Унитарные матрицы обобщают понятие ортогональных матриц, элементы которых — только действительные числа, на матрицы с комплексными числами.
Ортогональная матрица — это квадратная матрица A с вещественными элементами, результат умножения которой на транспонированную матрицу A^T равен единичной матрице:
AA^T = A^TA = E,
или, что эквивалентно, её обратная матрица (которая обязательно существует) равна транспонированной матрице:
A^-1 = A^T.
Комплексным аналогом ортогональной матрицы является унитарная матрица.

Однокубитные вентили описываются матрицами размера 2 × 2, двухкубитные — 4 × 4, а n-кубитные — 2ⁿ × 2ⁿ. Выстраивая их композиционно, можно производить требуемые квантовые вычисления над кубитами.
В отличие от классических логических вентилей, на входы квантовых вентилей подаются не бинарные сигналы, а векторы состояний, которые состоят из кубитов.

Квантовые вентили математически представляются унитарными матрицами, в которых число кубитов, подаваемых на вход и получаемых на выходе должно быть одинаковым.

При выполнении операции квантового вентиля над одним квантовым состоянием, можно получить другое квантовое состояние.

К началу страницы

Разберёмся “на пальцах”, как работает квантовый компьютер.

Кубит, самый важный элемент квантового компьютера, можно с физической точки зрения и для лучшего понимания, представить как магнит (атом или электрон), подвешенный в пространстве, который может вращаться по всем трем осям.

Само вращение магнита в пространстве – это и есть операции квантового компьютера.

При создании квантового компьютера принято решение, что если полюс магнита N (North) смотрит вверх – то это значение 0 (Ноль), а если вниз, то значение 1 (Единица). Математические операции с кубитом основаны на применении линейной алгебры в Гильбертовом пространстве.

Определяем, что такое значение кубита равное нулю (0).

Когда запускается квантовая программа, все кубиты с помощью внешнего магнитного поля выстраиваются в ноль (вверх).

После завершения квантовой программы, фактически после выполнения серии вращений кубитов, надо получить конечное значение кубитов (выполнить измерение), но это не так просто, так как кубиты крайне маленькие и нестабильные, на них негативно влияет тепловое излучение (поэтому их сильно охлаждают) и космические лучи. На кубит нельзя просто посмотреть и сказать, где у него сейчас полюс N. Измерение выполняется опосредованно, например, можно к кубиту (~~снизу и~~ ОЯ) сверху поднести магниты с полюсом N. Если полюс кубита N был направлен вверх, то кубит упадет вниз, и именно это падение можно зарегистрировать. То есть измерить, что состояние кубита равно 0 (Ноль). Сам кубит физически больше непригоден для дальнейшего использования в квантовой программе. В каждом квантовом компьютере измерение выполняется своими методами, но суть которых остается той же.

О суперпозиции.

Магнит может вращаться в любом направлении.

Начнём с того, что положим его на бок, повернув на 90⁰. Именно с этого и начинаются все квантовые алгоритмы.

При измерении такого, “повёрнутого” кубита, он будет падать вверх или вниз с вероятностью примерно 50%, которая зависит от точности построения квантового компьютера. Если кубит из вертикального положения повернуть не на 90^o, а только на пару градусов, то при измерении он с очень высокой вероятностью будет падать вниз (значение 0), а в редких случаях вверх (значение 1). То есть, любое отклонение от вертикали, приводит к возможности (вероятности) измерить единицу вместо нуля. Поэтому, исходную инициализацию кубитов и все вращения кубитов надо делать очень точно, надёжно защищая кубиты от внешнего воздействия. Иначе будет получаться ошибка вычислений. Современные квантовые компьютеры имеют крайне низкую точность, что является большой проблемой.
Укладывание кубитов (магнитов) на бок (поворот на 90⁰), это и есть перевод группы кубитов квантового регистра в состояние суперпозиции. Начиная с этого момента каждый (один) кубит хранит в себе значения 0–1 одновременно, два кубита хранят все значения от 0 до 3 одновременно, восемь кубитов все значения от 0 до 255 одновременно и т.д. Любое математическое действие над этой группой кубитов будет выполнено сразу для всех чисел, хранимых кубитами.
Допустим, что квантовый компьютер имеет два регистра по 32 кубита. Посчитаем сумму чисел из этих двух регистров. Выполнив сложение один раз, получаем абсолютно все возможные комбинации сумм чисел, которые только можно разместить в двух регистрах по 32 бита, т.е. было выполнено около 18 квинтиллионов операций сложения за одну физическую операцию (2⁶⁴ = 18 446 744 073 709 551 615). Чтобы эти значения получить, нужно выполнить Измерение. После измерения, квантовый компьютер выдаст один случайный результат из 18 446 744 073 709 551 615 возможных результатов.

Сам процесс измерения разрушит кубиты, и чтобы получить еще один результат, нам придется выполнить операцию заново.

Чтобы вытащить из квантовой машины все 18 квинтиллионов результатов, придется запустить его как минимум 18 квинтиллионов раз? Где суперпозиция, то есть одновременная “подача на блюдце” всех 18 446 744 073 709 551 615 – 1 возможных результатов?

О запутанности

Квантовая запутанность – это второй кит (после суперпозиции), на котором держится квантовый компьютер. Квантовая запутанность – эффект, который современная наука пока не может объяснить. Привычные условные переходы, циклы, умножение, деление, возведение в степень, тригонометрия недоступны для квантовых компьютеров, так как при измерении кубиты, содержащие исходные переменные, разрушаются.
Одна операция IF все же может быть выполнена, без проведения измерения: контролируемое NOT (CNOT), это аналог классической операции XOR. В этой операции участвуют два кубита, контролирующий и контролируемый. Все взаимодействие между кубитами сводится к операции CNOT.

Операция XOR (исключающее ИЛИ) – это логическая операция, которая применяется для сравнения двух битов или двух чисел в двоичной системе счисления.
Операция XOR возвращает истинное значение, когда только один из операндов истинный, а остальные операнды ложные.
Исключающее «ИЛИ» (XOR) – это строгая дизъюнкция, логическое вычитание (обозначение ^)

Если контролирующий кубит лежит на боку, то контролируемый будет либо повернут на 180 градусов с вероятностью 50%, либо останется в прежнем состоянии. Точное итоговое положение кубитов в 3D пространстве после такой операции не известно (они сразу во многих состояниях), ведь на кубиты нельзя посмотреть непосредственно. Но если запутанные кубиты измерить, то Q1 будет рандомно падать на сенсор 0 или 1, а Q2 будет всегда падать на противоположный сенсор. Почему так происходит, никто не знает. По логике, оба кубита лежат на боку, после операции CNOT они оба должны рандомно падать на оба сенсора, без какой-либо зависимости. По факту же, прослеживается четкая связь при измерении (с некоторой погрешностью, система все-таки аналоговая). На этот счет есть две теории.
По первой теории – кубиты обмениваются информацией между собой (неизвестно как, но мгновенно, больше скорости света). Когда первый кубит измеряют (бьют об сенсор), он сообщает второму кубиту куда именно упал, а тот его запоминает и при измерении ударится о противоположный сенсор.
По второй теории – при взаимодействии кубиты сразу договариваются, кто на какой сенсор упадет, происходит это за счет изменения физического параметра кубита, который науке пока не известен.

Подведём итог.

Запутать можно сразу много кубитов, и это обычное дело для квантовых компьютеров, для этого надо прогнать CNOT поочередно для нескольких кубитов.
После операции CNOT, контролирующий кубит на самом деле тоже меняет свою ориентацию в 3D пространстве. Его полюс N не двигается вверх-вниз, но сам кубит вращается вокруг оси Z, это явление называется Phase Kickback и оно имеет огромное значение для квантовых алгоритмов, именно оно дает ускорение вычислений. Об этом мы поговорим ниже.
Если после запутывания один из кубитов с помощью внешнего магнитного поля, перевести в состояние Ноль (повторить первичную инициализацию), то это никак не повлияет на второй кубит, состояние запутанности будет разорвано. Т.е. обмен информацией на сверхсветовой скорости, нельзя обеспечить за счет эффекта запутывания.

Образные сравнения для понимания

Запутанные частицы можно образно сравнить с носками: я надеваю один на правую ногу, второй автоматически становится левым.
Более корректное сравнение: запутанные частицы больше похожи на две монетки, стоящие на боку. Если одна из них упадет на “Орла”, то вторая почти наверняка упадет на “Решку”, даже по прошествии несколько часов. Объяснить это рационально невозможно.

К началу страницы

Как производятся вычисления на квантовом компьютере

Посмотрим, как выполняются вычисления на квантовом компьютере, пошагово:
1. На систему кубитов записывается начальное состояние.
2. Состояние системы или её подсистем изменяется посредством унитарных преобразований, выполняющих те или иные логические операции.
3. Измеряется значение, которое и является результатом работы квантового компьютера.

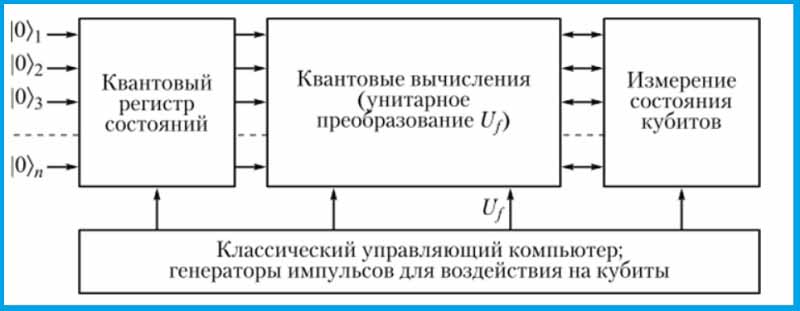
Роль проводов классического компьютера играют кубиты, а роль логических блоков классического компьютера – играют унитарные преобразования (U). Такая концепция квантового процессора и квантовых логических вентилей, была предложена в 1989 году, Дэвидом Дойчем. Также Дэвид Дойч в 1995 году, нашёл универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления.
Оказывается, что для построения любого вычисления, достаточно двух базовых операций. Квантовая система даёт результат, только с некоторой вероятностью являющийся правильным. Но за счёт небольшого увеличения операций в алгоритме, можно сколь угодно приблизить вероятность получения правильного результата к единице.
С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, любой квантовый компьютер решит, и почти за такое же время.
Большая часть современных ЭВМ работают по такой же схеме, а именно: n битов памяти хранят состояние и в каждый такт времени изменяются процессором. В квантовом случае, система из n кубитов находится в состоянии, являющемся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно.

К началу страницы

Программирования для квантовых компьютеров

Квантовое программирование связано с реализацией алгоритмов для квантовых компьютеров (квантовых алгоритмов).

Квантовый алгоритм – это классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами их надо совершать. Квантовый алгоритм задается либо в виде словесного описания таких команд, либо с помощью их графической записи в виде системы вентилей (quantum gate array). Результат работы квантового алгоритма носит вероятностный характер. За счёт небольшого увеличения количества операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.
Широко известные алгоритмы: Шора, Гровера, Дойча – Йожи, Залки – Визнера, Регева.

Квантовое программирование направлено на разработку алгоритмов, для решения некоторых типов задач, которые не могут быть эффективно решены классическими компьютерами. Одним из примеров применения квантового программирования, является создание безопасных криптографических систем. Кроме того, квантовое программирование находит применение в различных областях, таких как физика, биология и экономика, позволяя создавать новые материалы, оптимизировать производственные процессы и анализировать большие объемы данных.
Алгоритм Шора разработан Питером Шором в 1994 году, и представляет собой квантовый алгоритм, способный эффективно факторизировать большие целые числа.

Факторизация является процессом разложения числа на простые множители.

Факторизация больших чисел – причина уязвимости систем криптографии, которые до этого считались надежными.
Алгоритм Гровера (разработан Ловом Гровером) – это квантовый алгоритм, предназначенный для ускорения процесса поиска в неупорядоченных базах данных. Алгоритм применяет квантовые операции, такие как оракульная функция и квантовые амплитуды, для поиска нужного элемента в базе данных.

Оракул – это абстракция, вычисляющая за O(1) времени (за один такт машины Тьюринга), верно ли, что x принадлежит множеству A.

Алгоритм Гровера может примененяться в таких областях, как поиск в больших базах данных, оптимизация и распознавание образов.
При программировании алгоритмов используются специализированные языки программирования, позволяющие работать с кубитами (qubits) вместо классических битов. Квантовое программирование используется для решения сложных задач, которые не могут быть эффективно решены на классических (битовых) компьютерах.
Алгоритм Дойча – Йожи – это квантовый алгоритм, предложенный Дэвидом Дойчем и Ричардом Йожей в 1992 году, и ставший одним из первых квантовых алгоритмов. Алгоритм основывается на явлении квантовой запутанности и принципе суперпозиции, благодаря чему демонстрирует квантовое превосходство, то есть, значительно более эффективную работу в сравнении с известными классическими алгоритмами. Первый вариант алгоритма был разработан Дойчем в 1985 году, в нём рассматривается функция f(x) от одной переменной. Алгоритм Дойча не имеет практического применения в силу своей предельной простоты, зато является простейшим примером, с помощью которого можно понять, в чем состоит отличие квантовых алгоритмов от классических. Практически, алгоритм Дойча был реализован в 1998 году, на 2-кубитном квантовом компьютере, работавшем на принципах ядерно-магнитного резонанса. Алгоритм решает следующую задачу:

Дана “черная коробка” (или оракул), выполняющая некоторую неизвестную функцию, которая принимает один бит в качестве входа и возвращает один бит в качестве выхода. Существуют четыре возможных функции (две постоянные и две сбалансированные), и задача определить, является ли функция оракула постоянной или сбалансированной, используя оракул только один раз.

Простейшим примером сбалансированной булевой функции – функция, принимающая значение 1, если на входе четное число, и 0, если на входе нечетное число (или наоборот).

Языки программирования для квантовых компьютеров

Языки квантового программирования позволяют выражать квантовые алгоритмы с использованием высокоуровневых конструкций. Цель использования языков квантового программирования – предоставить средства для исследования и понимания работы квантовых вычислений.
Первым высокоуровневым языком программирования для квантовых компьютеров является язык Quipper, который основан на стандартизированном чисто функциональном языке программирования общего назначения Haskell. Quipper был опубликован в 2013 году и был реализован как встроенный язык с использованием Haskell в качестве основного языка. Поэтому, квантовые программы, написанные на Quipper, пишутся на Haskell с использованием предоставленных библиотек. Например, следующий код реализует подготовку суперпозиции:

import Quipper

spos :: Bool -> Circ Qubit
spos b = do q <- qinit b
            r <- hadamard q
            return r

В настоящее время, существует несколько языков для программирования на квантовых компьютерах, вот некоторые из них: QCL, Qiskit, Cirq, Microsoft Q#.
Quantum Computation Language (QCL) создан Бернхардом Омером в 1998 году. Развитие языка продолжается и сейчас: существует эмулятор, который позволяет запускать квантовые программы на классическом компьютере.

Qiskit – это открытый набор инструментов для разработки квантовых алгоритмов, созданный компанией IBM. Он включает в себя язык программирования Qiskit, который основан на Python и позволяет создавать и симулировать квантовые алгоритмы, а также реализовывать их на реальных квантовых устройствах.

Cirq — это открытый язык программирования квантовых вычислений, разработанный компанией Google. Основан на языке Python и предоставляет инструменты для создания квантовых алгоритмов и их реализации на реальных квантовых устройствах.

Microsoft Q# – это автономный язык, обеспечивающий высокий уровень абстракции. В нем нет понятия квантового состояния или цепи; вместо этого Q# реализует программы в терминах операторов и выражений, как в классических языках программирования. Предметно-ориентированный язык Q# (Q Sharp), используемый для выражения квантовых алгоритмов, впервые был представлен в составе Quantum Development Kit. Q# возможен для использования только как отдельно загружаемое расширение для Visual Studio. Quantum Development Kit поставляется вместе с квантовым симулятором, на котором может запуститься Q#. Для вызова квантового симулятора используется другой .NET Framework, который отдаёт входные (классические) данные в симулятор и забирает выходные (классические) данные из него.

Языки программирования для квантовых компьютеров

К началу страницы

Ещё немного философии, без которой не обойтись

Как всемирно известно, автор теории относительности, Альберт Эйнштейн, так и не смог понять и принять квантовую механику. И до наших дней эту теорию, которая успешно работает во многих областях физики и технологий, пытаются понять. С большим или меньшим успехом. То, что к удивлению работает и не поддаётся ясному пониманию самых выдающихся физиков теоретиков “огродили” и обозначили как “Философия квантовой механики” и приступили к её интерпретации, кто как сможет (понимает). Итак, квантовая механика считается “наиболее проверенной и наиболее успешной теорией в истории науки”, но согласия в понимании её глубинного смысла пока нет. Энгельс Чудинов, советский философ, специалист в области методологии науки, философских проблем физики, заметил, что: “У специалиста, работающего в области физики, часто возникает иллюзия полной независимости его научной деятельности от философии. Это происходит вследствие того, что он входит в уже готовое здание научной теории с присущим ей стилем научного мышления, и через стиль научного мышления воспринимает определённые философские принципы. Эти философские предпосылки научной теории не всегда ясно осознаются учеными, но от этого они не перестают быть философскими“.

Интерпретации квантовой механики

Интерпретация квантовой механики – это система философских воззрений на сущность квантовой механики, как физической теории, описывающей материальный мир. Известно несколько интерпретаций, по-разному решающих такие философские проблемы, как вопрос о природе физической реальности и способе её познания, о характере детерминизма и причинности, о сущности и месте статистики в квантовой механике. Интерпретации, которые наиболее поддерживаемые профессиональным научным сообществом (в скобках процент опрошенных специалистов):
1. Копенгагенская (~ 27%). Сформулировали Нильс Бор и Вернер Гейзенберг, в 1927 году. Согласно копенгагенской интерпретации, квантовая механика описывает не микрообъекты сами по себе, а их свойства, проявляющиеся в макроусловиях, создающихся классическими измерительными приборами, в процессе акта наблюдения.
2. Многомировая или интерпретация Эверетта (~ 17%). Сормулировал Хью Эверетт, в 1957 году. Интерпретация предполагает существование, в некотором смысле, «параллельных вселенных», в каждой из которых действуют одни и те же законы природы и которым свойственны одни и те же мировые постоянные, но которые находятся в различных состояниях.
3. Де Бройля — Бома (волны-пилота) (~ 8%). Теория волны-пилота была представлена Луи де Бройлем в 1927 году. Её более современная версия в интерпретации Бома, является попыткой интерпретации квантовой механики как детерминированной теории, в которой находят своё объяснение такие понятия, как мгновенный коллапс волновой функции и парадокс кота Шредингера.

Детерминизм — философская концепция о взаимосвязи и взаимной определённости всех явлений и процессов, доктрина о всеобщей причинности.
Кот Шрёдингера — мысленный эксперимент, предложенный одним из создателей квантовой механики Эрвином Шрёдингером в 1935 году, при обсуждении физического смысла волновой функции. В ходе эксперимента возникает суперпозиция живого и мёртвого кота, что выглядит абсурдно с точки зрения здравого смысла.

4. Другие интерпретации: Супердетерминизм, Реляционная, Объективная редукция, Квантовое байесианство, Транзакционная, Фон Неймана — Вигнера, Блохинцева, Фока.

Заключение

В заключении перечислим трудности, которые стоят перед квантовыми компьютерами.
1. Сложность технической реализации. Квантовая запутанность, которая используется в большинстве компьютеров — крайне нестабильное состояние. Любое внешнее воздействие разрушает эту связь. Именно поэтому ученые вынуждены строить специальные саркофаги, в которых поддерживается температура близкая к абсолютному нулю (-273,14 °C). И это не говоря о радиационной и электромагнитной защите.

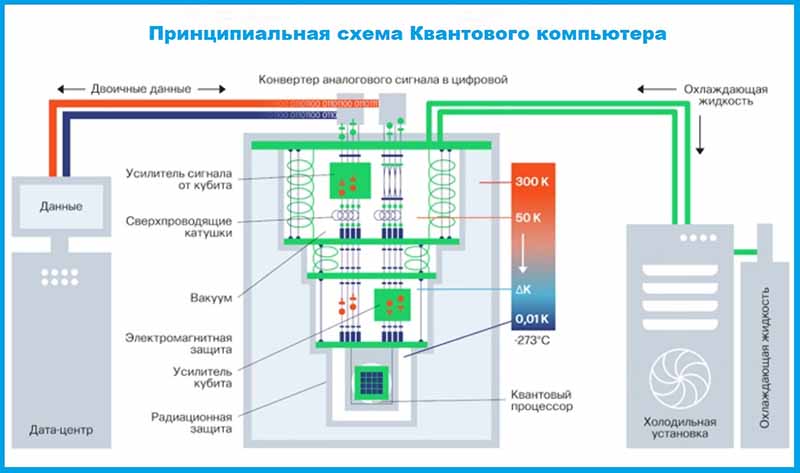
Принципиальная схема Квантового компьютера

2. Кратковременность стабильной системы. В среднем спутанные частицы существуют до 200 микросекунд. То есть, за это время необходимо успеть инициализировать систему, провести вычисления и считать итоговый результат. Если промедлим — на выходе получим шумы.
3. Ошибки, которые могут появиться из-за плохой изоляции рабочей камеры, когда случайная частица проникнет в систему. Возможны также ошибки работы квантовых вентилей и даже во время считывания результата. Причем процент ошибок увеличивается пропорционально числу кубитов, что усложняет создание многокубитных квантовых компьютеров.
4. Сложность архитектуры. Связать два кубита не проблема, но если у вас их около сотни, то все намного сложнее. Сейчас же один кубит может быть связан максимум с шестью соседями. Именно поэтому приходится строить сложные схемы связей, чтобы получить многокубитные процессоры.
5. Специфичность. Квантовые компьютеры эффективнее обычных только в отдельных задачах и только с применением специальных алгоритмов. В пользовательских приложениях, вроде просмотра мультимедийного контента, серфинга в сети и так далее квантовые вычисления пока не дают никаких преимуществ.

Если попытаться оценить, на каком ступени развития находятся квантовые компьютеры, в терминах поколений привычных нам компьютеров, то современные квантовые компьютеры – это даже не первое поколение, а на подходе к первому поколению.

В настоящее время, ни один квантовый компьютер не может выполнить полезную задачу быстрее, дешевле или эффективнее, чем классический. Квантовое преимущество – это порог (и к нему стремятся разработчики), при достижении которого созданная нами квантовая система может выполнять операции, которые лучший из возможных классических компьютеров не может смоделировать за любое разумное время. Посмотрите фильм – фантазию о квантовом компьютере будущего.

Видео: Квантовый компьютер будущего (Devs) в действии. Многомировая интерпретация.

Некоторые определения

Квантовое вычисление, есть контролируемая классическим управляющим компьютером последовательность унитарных операций простого вида (над одним, двумя или тремя кубитами). В конце вычисления состояние квантового процессора измеряется, что и даёт искомый результат вычисления. Основные принципы квантовой механики, которые лежат в основе квантовых вычислений, включают принцип суперпозиции, принцип запутанности и принцип измерения. Квантовые вычисления с физической точки зрения оперируют с квантовыми системами и используют кубиты, которые могут находиться в состоянии суперпозиции и обладать квантовой взаимосвязью между собой — квантовой запутанностью.
Квантовый параллелизм в вычислении. Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса квантового вычисления преобразуется в классическую, путём измерения конечного состояния кубитов квантового регистра. Выигрыш в квантовых алгоритмах достигается за счёт того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно.
Принцип суперпозиции . Суперпозиция, как возможность нахождения во многих состояниях одновременно – это базовое понятие квантовых вычислений. Кубит может находиться в состоянии суперпозиции, то есть, одновременно в нескольких состояниях. Принцип суперпозиции означает, что кубиты могут существовать одновременно во всех возможных состояниях, пока не производится измерение, когда будет определено конкретное состояние.

Принцип Суперпозиции (принцип наложения) – это допущение, согласно которому если составляющие сложного процесса воздействия взаимно не влияют друг на друга, то результирующий эффект будет представлять собой сумму эффектов, вызываемых каждым воздействием в отдельности. Принцип Суперпозиции строго применим к системам, поведение которых описывается линейными соотношениями (так называемые линейные системы).

Квантовая запутанность – это уникальное свойство квантового мира, когда частицы (связанные друг с другом, то есть запутанные) могут “чувствовать” друг друга на расстоянии и мгновенно менять свое состояние в ответ на изменение состояния другой частицы. Это явление используется для передачи и обработки данных. Принцип запутанности описывает взаимосвязь между кубитами, когда изменение одного кубита немедленно влияет на другие кубиты, вызывая эффекты суперпозиции и интерференции.
Принцип измерения позволяет получить определенное значение измеряемой величины кубита, что определяет конечный результат вычисления.
Квантовое превосходство (преимущество) – это способность квантовых вычислительных устройств решать проблемы, которые классические компьютеры практически не могут решить.
Декогеренция – это явление, при котором квантовая система взаимодействует с окружающей средой, что приводит к потере квантовых свойств (потере квантового состояния в кубите) и, следовательно, к ухудшению точности и стабильности вычислений.. Факторы окружающей среды, такие как радиация, могут вызвать коллапс квантового состояния кубитов. Большой инженерной задачей при создании квантового компьютера, является разработка различных функций, которые пытаются задержать декогеренцию состояния, например, создание специальных структур, экранирующих кубиты от внешних полей.
Логический вентиль – это базовый элемент цифровой схемы, выполняющий элементарную логическую операцию, преобразуя множество входных логических сигналов в выходной логический сигнал. Логика работы вентиля основана на битовых операциях с входными цифровыми сигналами, в качестве операндов. При создании цифровой схемы, вентили соединяют между собой, при этом, выход используемого вентиля, должен быть подключён к одному или к нескольким входам других вентилей. В цифровых устройствах в качестве логических вентилей, используют транзисторы, электромагнитные реле, гидравлические устройства, механические устройства. В поисках более совершенных логических вентилей исследуются квантовые устройства, биологические молекулы, фононные тепловые системы. В цифровой электронике логический уровень сигнала представлен в виде уровня напряжения (попадающего в один из двух диапазонов) или в виде значения тока. Это зависит от типа используемой технологии построения электронной логики. Поэтому, любой тип электронного вентиля требует наличия питания для приведения выходного сигнала к необходимому уровню.
Квантовый вентиль или квантовый логический элемент – это базовый элемент квантового компьютера, преобразующий входные состояния кубитов на выходные по определённому закону. Отличается от обычных логических вентилей тем, что работает с кубитами. Квантовые вентили, в отличие от многих классических, всегда являются обратимыми. Так как кубит можно представить вектором в двумерном пространстве, то действие вентиля можно описать унитарной матрицей (матрица унитарна тогда и только тогда, когда существует обратная к ней матрица), на которую умножается соответствующий вектор состояния входного кубита. Однокубитные вентили описываются матрицами размера 2 × 2, двухкубитные — 4 × 4, а n-кубитные — 2ⁿ × 2ⁿ.
Квантовая машина Тьюринга или универсальный квантовый компьютер – это абстрактная машина, используемая для моделирования квантового компьютера, представляет собой простую модель, которая может описать любые квантовые вычисления. Любой квантовый алгоритм может быть формально описан, как некоторая квантовая машина Тьюринга. Впервые построена в 1985 году Дэвидом Дойчем, обратившим внимание на аналогию между квантовыми вентилями и логическими вентилями в цифровых схемах. Большое распространение получила модель квантовых схем (модель квантовых вычислений, аналогичная классическим схемам, в которых вычисление представляет собой последовательность квантовых вентилей, измерителей, инициализации кубитов известными значениями и, возможно, других действий), вычислительно эквивалентная квантовой машине Тьюринга, но более удобная для исследовательских целей.
Масштабируемость квантовых систем. В настоящее время, у нас есть квантовые компьютеры с небольшим числом кубитов, однако для решения реальных задач требуется значительное увеличение их мощности. Разработчикам необходимо искать пути увеличения числа кубитов и улучшения их производительности, чтобы обеспечить масштабируемость и применение квантовых систем для решения широкого спектра задач.