Оглавление
История возникновения концепции КМ
Вещественный стул
Стояла задача соединить реальный стул с его семантическим представлением в сознании человека. Были предложены описания всех свойств стульев в виде множеств.
Множество всех свойств всех вещественных стульев обозначим:
P = {Pi}i=1 n
Членами этого множества окажутся, например, такие свойства:
{железный, деревянный, пластиковый, трёхножный, четырёхножный, со спинкой, без спинки…….}
Множество свойств конкретного типа стула является подмножеством множества всех свойств всех стульев:
Tk (p) ⊂ P , где T – тип стула.
Кстати, попутно мы можем поставить интересную задачу определить что такое стул «вообще», некая экзистенция стула.
Гипотеза: пересечение всех свойств всех типов стульев будет множество определяющее экзистенцию стула EC:
EC = ⋂k Tk(P)
Мы предложили, что существуют свойства общие для всех стульев. Т.е. во-первых, человечество создав стулья реализовало общую для всех стульев функцию; во-вторых, создав слово «стул» человечество смогло из множества свойств стульев выделить что-то общее.
Стул, это семейство множеств, смысл стула – пересечение всех множеств свойств стула.
Мнимый стул
Все свойства, все типы стульев и «стул вообще» – «прописаны» в сознании человека.
В формуле P = {Pi}i=1 n в множестве P содержатся все физические свойства всех типов стульев x. Для отображение множества P в сознании человека используем обозначение отображенного множества обозначение VP (Virtual Properties). Тогда
VP = {VPi}i=1 n
Следует отметить, что множества P и VP не будут иметь равную мощность и не будут биективными, так как могут быть неизвестные, не названные свойства реальных стульев, так и могут быть придуманные свойства стульев в сознании человека, которые ещё не воплощены в реальности или не будут никогда воплощены.
Далее, возникла идея, что два множества P и VP образуют семейство множеств FC (Family Chairs) состоящее из двух множеств:
FC=〖{{P_i }_(ⅈ=1)^n,{VP_j }〗_(j=1)^m}
FC={P,VP}
Первоначально казалось, что семейства множеств достаточно для описание свойств дуальной сущности стула вещественного и стула символического:
X={{A}_n,{B}_m }
Но довольно скоро возникла концепция создать Комплексное множество, где мнимая часть, как в комплексном числе, маркирована мнимой единицей, что достаточно эффективно позволяет моделировать разную природу дуальности соединяющей реальные объекты и их символы в сознании.
Таким образом человечеством изобретено и воплощено в реальности два стула: один в вещественной реальности, другой в мнимой, информационной реальности или реальности сознания.
Искусственные (сотворённые множества)
S I T A
Предлагается для использования множество A – множество всех вещей, предметов, символов и образов, созданных человеком – т.е. вся созданная реальность, как физическая, так и символическая. Человек может создавать предметы, и может создавать символы.
В него входят два подмножества S и T:
Множество S – множество всех символов, образов, всего, что может существовать только в человеческом сознании и человеческом обществе. Также S существует в информационном виде или в информационном пространстве Вселенной – I.
Множество T – множество вещей, веществ – всего не символического, то, с чем может осуществляться материальное и энергетическое взаимодействие.
S ⊂ A
S ⊂ I
T ⊂ A
I ⊂ U
A ⊂ U
Где U – универсальное множество всех множеств во Вселенной
Создание артефакта стула, это создание двойной сущности. Всё создаётся дважды. Создан комплексный стул одновременно в вещественной реальности и в мнимой, символьной реальности человеческого сознания.
Поскольку любое множество можно рассматривать как частный случай КМ, в котором мнимая часть равна нулю, тогда можно оставить традиционное обозначение множества всех КЧ и КМ как универсума, который мы расширяем на КМ.
В теории комплексных множеств мы можем говорить о существовании пространств физических и мнимых – информационных.
Применение КМ в физике – Троица взаимодействия
Любые два взаимодействующие объекта образуют тройственность. Например, два гравитационно взаимодействующих физических тела – два тела и сила притяжения между ними. Как бы мы ни уменьшали количество объектов во взаимодействии, мы не можем получить менее двух объектов. В самой сущности элементарного взаимодействия лежат две точки и соединяющий их вектор. Представить себе одно тело с гравитационным полем в полном отсутствии других тел можно, но вряд ли такая модель имеет какое-то отношение к Вселенной, в которой мы находимся.
КМ хорошо моделирует такую тройственность через свои два внутренних множества и возможность отображений этих множеств друг на друга.
Два объекта и сила взаимодействия между ними – это неделимая сущность при этом имеющая внутреннюю структуру.
Свойство взаимодействия определяется составом множеств входящих в КМ. Таким образом можно сделать вывод о том, что все силы во Вселенной определяются составом объектов. Также можно говорить о том, в рамках философии КМ, что физический профиль взаимодействия определяется физическими профилями двух тел входящих в это взаимодействие. Для всех четырех фундаментальных взаимодействий характерно наличие двух зарядов и силы между ними. Сила всегда носит векторный характер. Между любыми двумя точками поля мы можем провести вектор силы:
1. Гравитационное: Материальные тела (материальные заряды) притягиваются.
2. Электромагнитное: Заряженные тела (электромагнитные заряды) либо притягиваются, либо отталкиваются.
3. Сильное: Цветной заряд.
4. Слабое: Слабый изоспин.
Любое взаимодействие можно спроектировать на модель КМ, где внутренние множества описывают параметры или свойства зарядов, а отображение описывает параметры, характер действующей силы.
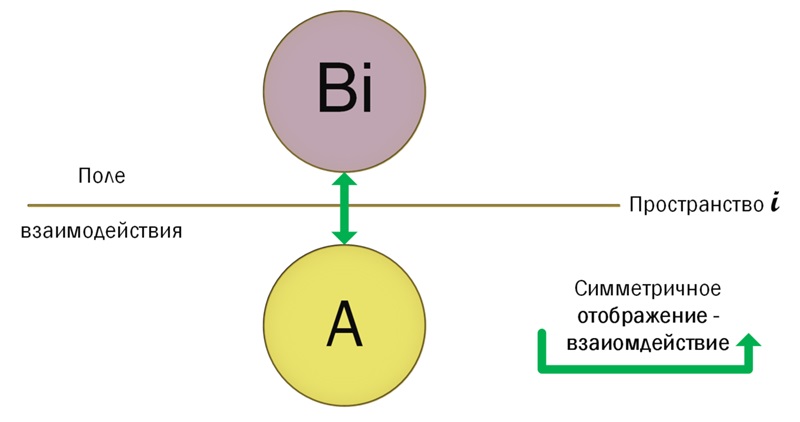
Для двух электронов A = B – оба множества описывают два одинаковых электрона отличающихся либо импульсом, либо координатами. Отображение-взаимодействие определяется только составом множеств А и B.
Мы не уверены в перспективности использования КМ в физике, но надеемся на исследователей физики, которые могут проверить эту возможность.
Комплексная плоскость
КМ можно представить как два многомерных пространства связанных через комплексную плоскость.
Дальнейшие уточнения этого заявления требуют дополнительных исследований.
Альтернативная нотация для обозначения КМ
Обозначения КМ
Кроме стандартной нотации X=A+Bi можно попробовать использовать следующую нотацию:
X = {A, Bi} или X = (A, Bi)
Не исключено, что на основе Теории КМ можно переосмыслить, как сущность КЧ, так и их нотацию. Например, для комплексных чисел можно, как альтернативу использовать запись
z = (a, bi)
Двойная нотация операций с КМ
Для уровня отношений между КМ можно примерить удобство использования для операций с КМ следующих видов двойной нотации:
⋓ Двойное объединение. Юникод U+22D3;
⋒ Двойное пересечение. Юникод U+22D2;
⋐ Двойное подмножество. Юникод U+22D0;
⋑ Двойное надмножество. Юникод U+22D1/
Пример:
Пусть X=A+Bi и Y=C+Di являются КМ, тогда допустима следующая нотация для операций с КМ:
X ⋓ Y = (A ∪ B) + (C ∪ D)i или X ⋓ Y = {(A ∪ B),(C ∪ D)i};
X ⋒ Y = (A ∩ B) + (C ∩ D)i или X ⋒ Y = {(A ∩ B),(C ∩ D)i};
X ⋐ Y = (A ⊂ B) + (C ⊂ D)i или X ⋐ Y = {(A ⊂ B),(C ⊂ D)i};
Виды КМ:
1. Произвольные КМ (общий случай).
2. Обычные множества (как частный случай КМ).
3. Числовые (как частный случай КМ).
3.1. Натуральные.
3.2. Вещественные.
3.3. Комплексные числа (как частный случай числовых КМ).
4. Родственные.
4.1. Внутри-родственные.
4.1.1. Тождественно-родственные.
4.1.2. Родственные по мощности.
4.2. Внешне-родственные.
4.2.1. Равные.
4.2.2. Равно-мощные.
4.2.3. Смешанные.
4.2.4. Смешанные для двух КМ.
4.2.4.1. Двоюродные.
4.2.4.2. Троюродные.
5. Внутрипересекающиеся.
Примеры формул по некоторым видам КМ:
Равные A = B = C = D ⇔ X = Y
Равно мощные |A| = |B| = |C| = |D| ⇔ |X| = |Y|
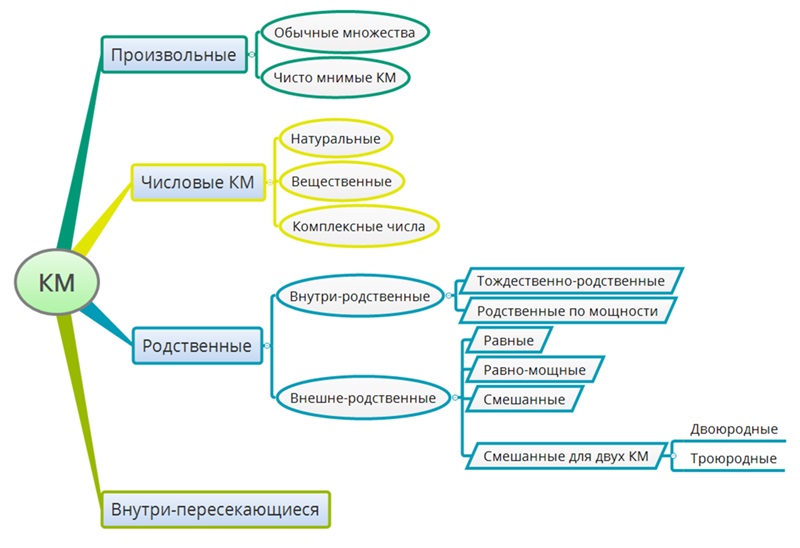
Таблица используемых математических символов
∀ квантор всеобщности (\forall, «Для любых», «Для всех», «Для всякого»);
| множество элементов, удовлетворяющих условию («Множество всех… таких, что верно…»);
∧ «и» (\wedge, Конъюнкция);
∨ Дизъюнкция (\vee, «или», A ∨ B истинно, когда хотя бы одно из условий A или B истинно.)
∈ принадлежность к множеству (\in, «принадлежит», «из»);
⋃ Объединение (\cup, «Объединение … и …», «…, объединённое с …», A ⋃ B означает множество, содержащее все элементы из A и B);
∩ Пересечение (\cap, «Пересечение … и …», «…, пересечённое с …», A ∩ B означает множество одинаковых элементов, принадлежащих и A, и B);
⊂ Подмножество (\subset, «является подмножеством», «включено в») (A ⊂ B обычно означает то же, что и A ⊆ B);
⊆ Подмножество (\subseteq, A ⊆ B означает «каждый элемент из A также является элементом из B».)
Импликация, следование (\Rightarrow, A
B означает «если A верно, то B также верно».);
⋐ Двойное подмножество (Double Subset), представленное как ⋐, — это математическое обозначение, часто используемое в теории множеств. Этот символ представляет концепцию, в которой один набор не только является подмножеством другого, но также, возможно, равен ему;

N – Натуральные числа;
Z – Целые числа
Q– Рациональные числа;
R – Вещественные (действительные) числа;
C – Комплексные числа;
∖ Разность множеств (\setminus, «разность … и …», «минус», «… без …», A ∖ B означает множество элементов, принадлежащих A, но не принадлежащих B, {1,2,3,4) \ {3,4,5,6} = {1,2});
⇔ Равносильность (\Leftrightarrow, «если и только если» или «равносильно», A ⇔ B означает «A верно тогда и только тогда, когда B верно»).